Having studied the macroscopic movement of a system of particles, we now turn to
the microscopic movement: the movement of individual particles in the system.
This movement is determined by forces applied to each particle by the other
particles. We shall examine how these forces change the motion of the
particles, and generate our second great law of conservation, the conservation
of linear momentum.
Impulse
Often in systems of particles, two particles interact by applying a force to
each other over a finite period of time, as in a collision. The physics of
collisions will be further examined in the next
SparkNote as an extension of our
conservation law, but for now we will look at the general case of forces acting
over a period of time. We shall define this concept, force applied over a time
period, as impulse. Impulse can be defined mathematically, and is denoted
by J:
Just as work was a force over a distance,
impulse is force over a time. Work applied mostly to forces that would be
considered external in a system of particles: gravity, spring force, friction.
Impulse, however, applies mostly to interactions finite in time, best seen in
particle interactions. A good example of impulse is the action of hitting a
ball with a bat. Though the contact may seem instantaneous, there actually is a
short period of time in which the bat exerts a force on the ball. The impulse
in this situation is the average force exerted by the bat multiplied by the time
the bat and ball were in contact. It is also important to note that impulse is
a vector quantity, pointing in the same direction as the force applied.
Given the situation of hitting a ball, can we predict the resultant motion of
the ball? Let us analyze our equation for impulse more closely, and convert it
to a kinematic expression. We first substitute F = ma into our equation:
J = FΔt = (ma)Δt
But the acceleration can also be expressed as
a = 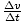
.
Thus:
J =
m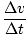 Δt
Δt =
mΔv =
Δ(
mv) =
mvf -
mvo
The large impulse applied by the bat actually reverses the direction of the
ball, causing a large change in velocity.
Recall that when finding that work caused a change in the quantity
 mv2 we defined this as kinetic energy. Similarly, we define
momentum according to our equation for an impulse.
mv2 we defined this as kinetic energy. Similarly, we define
momentum according to our equation for an impulse.
Momentum
From our equation relating impulse and velocity, it is logical to define the
momentum of a single particle, denoted by the vector p, as such:
Again, momentum is a vector quantity, pointing in the direction of the velocity
of the object. From this definition we can generate two every important
equations, the first relating force and acceleration, the second relating
impulse and momentum.
Equation 1: Relating Force and Acceleration
The first equation, involving calculus, reverts back to Newton's Laws. If we
take a time derivative of our momentum expression we get the following equation:
Thus
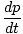 = = 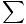 F F |
|
It is this equation, not
F = ma that Newton originally used to relate force and
acceleration. Though in classical mechanics the two equations are equivalent,
one finds in relativity that only
the equation involving
momentum is valid, as mass becomes a variable quantity. Though this equation is
not essential for classical mechanics, it becomes quite useful in higher-level
physics.