Geometry: Triangle Inequality and Angle-Side Relationship
Related Pages
Types Of Triangles
Classifying Triangles
Special Right Triangles
More Geometry Lessons
In these lessons, we will learn two commonly used inequality relationships in a triangle:
- the Triangle Inequality Theorem,
- the Converse of the Triangle Inequality Theorem,
- the Angle-Side Relationship for triangles.
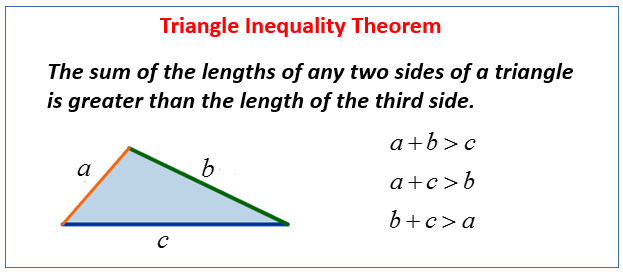
The Triangle Inequality Theorem is a fundamental principle in geometry that states a crucial condition for three given line segments to form a triangle: The sum of the lengths of any two sides of a triangle must be greater than the length of the third side
The following diagrams show the Triangle Inequality Theorem and Angle-Side Relationship Theorem. Scroll down the page for examples and solutions.
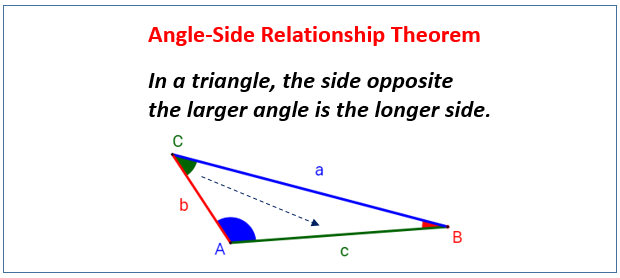
The Angle-Side Relationship Theorem (sometimes called the Angle-Side Inequality Theorem or the Side-Angle Inequality Theorem) describes a fundamental relationship between the angles and the lengths of the sides opposite those angles within any given triangle.
Triangle Inequality Theorem
The Triangle Inequality theorem states that
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
The Converse of the Triangle Inequality theorem states that
It is not possible to construct a triangle from three line segments if any of them is longer than the sum of the other two.
Example 1: Find the range of values for s for the given triangle.
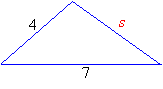
Solution:
Step 1: Using the triangle inequality theorem for the above triangle
gives us three statements:
s + 4 > 7 ⇒ s > 3
s + 7 > 4 ⇒ s > –3
(not valid because lengths of sides must be positive)
7 + 4 > s ⇒ s < 11
Step 2: Combining the two valid statements:
3 < s < 11
Answer: The length of s is greater than 3 and less than 11
What is the Triangle Inequality Theorem?
The following video states and investigates the triangle inequality theorem.
The sum of lengths of any two sides of a triangle must be greater than the length of the third.
We really only need to make sure the sum of the lengths of the two shorter sides is greater
than the length of the longest side.
Examples:
Which lengths can form a triangle?
- 3, 4, 6
- 5, 6, 11
- 2, 3, 9
Description of the Triangle Inequality
The following video describes triangle inequality by trying to construct triangles with different
length segments.
What are the conditions required to draw a triangle to illustrate triangle inequality?
Intuition behind the triangle inequality theorem
Angle-Side Relationship
The Angle-Side Relationship states that
The longest side of a triangle is always opposite the largest angle.
The shortest side of a triangle is always opposite the smallest angle.
This also means that equal angles are opposite equal sides (for example in isosceles/equilateral triangles).
Example 1: Compare the lengths of the sides of the following triangle.
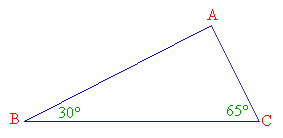
Solution:
Step 1: We need to find the size of the third angle. The sum of all
the angles in any triangle is 180º.
∠A + ∠B + ∠C = 180°
⇒ ∠A + 30° + 65° = 180°
⇒ ∠A = 180° - 95°
⇒ ∠A = 85°
Step 2: Looking at the relative sizes of the angles.
∠B < ∠C < ∠A
Step 3: Following the angle-side relationship we can order the sides accordingly. Remember it is the side opposite the angle.
![]()
Answer: ![]()
Examples of the angle-side relationships in triangles
Angle side relationships in Triangles
If 2 sides of a triangle are not congruent, then the larger angle is opposite the larger side.
If 2 angles of a triangle are not congruent, then the larger side is opposite the larger angle.
The measure of Angle A is greater than the measure of Angle B, and the measure of Angle B is
greater than the measure of Angle C. Find the possible values for the length of side AC.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.